What is percent/percentage?
Introduction
The word percent is derived from the Latin word ‘per centum’ meaning ‘by the hundred’. A percentage is a portion of the whole expressed as a fraction of one hundred. It is a relative value indicating the hundredth parts of a quantity, ratio or number.
In the simplest terms, percent means ‘out of one hundred’ or ‘by hundred’.
- One percent (1%) means 1 per hundred or 1⁄100
- Five percent (5%) means 5 per hundred or 5⁄100
- Thirty-three (33%) percent means 33 per hundred or 33⁄100
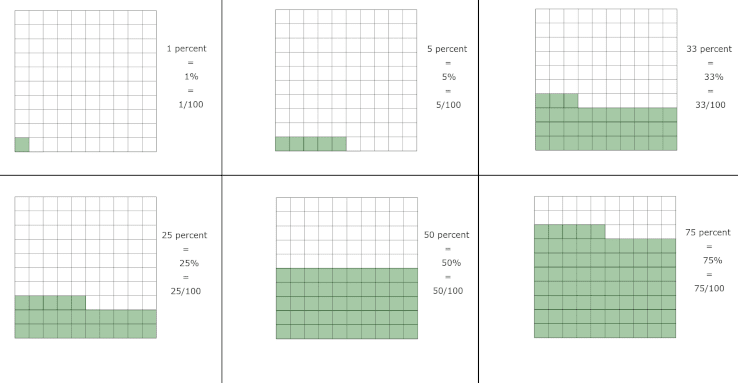
The ability to quantify things as a fraction of one hundred let’s us get a way better understanding of the ratios or numbers involved. Percentages are very commonly used and are a necessity in day-to-day life. The use of percentages makes a lot of things much easier.
Example: Assume we have to calculate and compare the passing rates of two different tests. In Test A, 25 students out of 50 pass the test. In Test B, 6,876 students out of 14,323 pass the test.
Without the use of percentages, it would be difficult to express what fraction of the students passed the tests as well as to compare which test has a higher or lower passing rate. In Test A, you might easily say ‘Half the students passed the Test’ but in Test B, it is very difficult to express the same. You cannot always express things in fractions of a quarter, a half or three-fourths. At the same time it is also very difficult to compare the Tests when there is a large difference between the scores like the above example where in one test 25 students out of a batch of 50 pass it compared to the second test where 6876 students out of a batch of 14,323 pass the test.
This is where percentages are really useful. When the above passing numbers are expressed as percentages, we get that the passing percentage of Test A is 50%. And despite the bigger numbers, the passing percentage of Test B is 48% and actually lower than that of Test A. (Don’t worry about the calculations behind how we got the percentages for now, that will be covered in detail below soon)
This ability to express non-hundreths in terms of hundreths is an extremely useful and essential one crucial to almost all fields of business, mathematics and life today. This ability of a portion of the whole expressed as a percentage let’s us easily calculate and understand a lot of things very easily like percentage increase, decrease or change etc. All of which we will study in detail later.
Percentage symbol
Percentage is most commonly denoted by the symbol ‘%’ which is called as the percent sign. In rare instances percentage can also be denoted by abbreviations like ‘p.c.’, ‘pc’, ‘pct’ and ‘pct.’
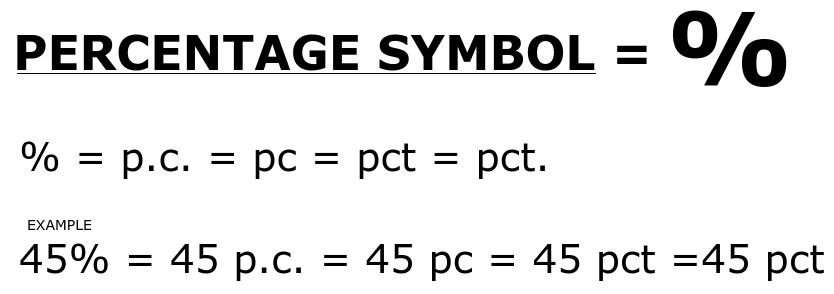
Percent vs percentage
The word ‘Percent’ and ‘Percentage’ are closely related often used interchangeably especially in mathematics assuming it does not make much of a difference and true, that they won’t affect your calculation but semantically, the two terms are not the same and incorrect usage often the terms makes them sound wrong.
‘Percent’ – Percent is a unit of measurement used to express a specific number that is being expressed. (Think, like metres or kilograms) and it preceeded by an number or amount.
For example: “In a county in USA, only 30 percent of voters showed up to vote for the candidates at the booth” or “twenty five percent of houseowners in…” or “12 percent of runners participating in…”
‘Percentage‘ – Percentage is more commonly used to express the degree of a part out of the whole and is not preceeded by a number but rather is preceeded by non-specific terms.
For example, “In a county in USA, a large percentage of voters did not show up to vote” or “A certain percentage of home-owners” or “A small percentage of runners participating in..”
Percentage formula
There are a few different ways that percentage problems are presented and based on that, the formula for calculating percentage varies. Let us look at each one below
Percent of whole
Percent of whole problems are one where the ‘whole’ is provided and you have to calculate a ‘part’ of it depending on the percentage which is also provided. In simple words, you have to calculate what part of the whole corresponds to the respective percentage.
Example problem statements:
- What is 20% of 300?
- What is 50% of 100 acres?
The formula to find a part of the whole based on a certain percentage is:
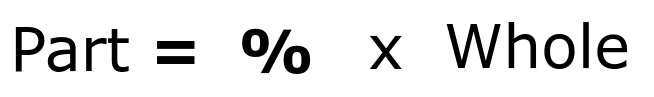
As can be seem above, you simply have to multiply the percentage by the whole to get the part. But remember, percentage always means ‘by hundred’. So for instance, if you have to multiply by 21%, you will multiply by 0.21 and not by 21 because 21% = 21⁄100 = 0.21
Let us better understand the usage of the above formula with some examples and solve them step-by-step
Example a) What is 25% of 300?
Solution: Percentage = 2%, ‘Whole’ = 300
Substituting the same in the above formula, we get
Part = Percentage x Whole
= 25% x 300
= 25⁄100 x 300
= 0.25 x 300
= 75
Answer: 25 percent of 300 is 60
Example b) What is 45% of 100 acres?
Solution: Percentage = 45%, ‘Whole’ = 100
Substituting the same in the above formula, we get
Part = Percentage x Whole
= 45% x 100
= 45⁄100 x 100
= 0.45 x 100
= 45
Answer: 45% of 100 acres is 45 acres
Example c) A soccer player scores a goal 53% of the time he takes a penalty kick. If the soccer player has shot 85 penalty kicks over the course of his lifetime, then calculate the number of times he has scored a penalty kick goal.
Solution: Percentage = 53%, ‘Whole’ = 85
Substituting the same in the above formula, we get
Part = Percentage x Whole
= 53% x 85
= 53⁄100 x 85
= 0.53 x 85
= 45.05
Answer: The soccer player has scored a penalty kick goal 45 times that he has taken it
How to Calculate Percentage Using A Calculator
You can easily calculate percentages using any basic or advanced calculator. You can also use the calculator available in your PC or on your mobile phones. You can calculate the percentage using both the percentage function and without the percentage function. See the video given below to learn how:
Tricks, Shortcuts and Mental Math Tricks to Calculate Percentage
Splitting trick
The splitting trick is a fast way to mentally calculate percentages by breaking the percentage into parts of 10% and 1%. 10% of something is simply, one decimal to the left and 1% of something is simply two decimals to the left. Let us understand the same with an example
You can also use the same method to calculate percentages that end in six, seven, eight and nines like 49%, 67%, 99%, 88% etc by subtraction the ‘ones’ from the next ‘tens’ value
Example a) What is 33% of 600?
10% → 60
30% → 180
1% → 6
3% → 18
Therefore, 33% = 30% + 3% = 180 + 18 = 196
Answer: 33% = 196
Example b) What is 38% of 1400?
10% → 140
40% → 560
1% → 14
2% → 28
Therefore, 38% = 40% – 2% = 560 – 28
Answer: 38% = 196
Commutativity
For percentages, the property of commutativity applies
Example: 10% x 250 = 10 x 250% = 25
Hence whenever you are presented with difficult to calculate percentage, you can use the commutativity property to calculate percentage faster. Let us understand the same using an example
Example: What is 44% of 75?
Solution: Calculating 75% or three-fourths of something, especially a number like 44 than can easily be divided into 4 parts, is a lot easier than calculating 44% of 75.
Hence, using the property of commutativity, we get:
44% of 75 = 75% of 44 = 33 (Break 44 into 4 equal parts of 11 and multiply by 3)
Quarter, Halfs and Wholes
When you are presented with percentage values like 1%, 10%, 25%, 50%, 200% etc, it is a lot more easier to calculate the answer mentally (and most times faster than using a calculator unless you’re calculating very big numbers or decimals) than compared to percentage values like 13%, 17%, 69%, 73%,…etc
| Percentage | Shortcut | Example |
| 1% | Shift Two Decimals To The Left | 1% Of 400 = 4.00 |
| 10% | Shift One Decimal To The Left | 10% Of 400 = 40.0 |
| 12.5% | Divide The Whole By 8 | 12.5% Of 400 = 50 |
| 20% | Divide The Whole By 5 | 20% Of 400 = 80 |
| 25% | Divide The Whole By 4 | 25% Of 400 = 100 |
| 50% | Divide The Whole By 2 | 50% Of 400 = 200 |
| 75% | Divide The Whole By 4 And Multiply The Result By 3 | 75% Of 400 = 100 X 3 = 300 |
| 100% | The Number Itself | 100% Of 400 = 400 |
| 125% | Divide The Whole By 4 And Multiply The Result By 5 Or Directly Multiply The Whole By 1.25 | 125% Of 400 = 100 X 5 = 500 |
| 150% | Divide The Whole By 2 And Multiply The Result By 3 Or Directly Multiply The Whole By 1.5 | 150% Of 400 = 200 X 3 = 600 |
| 175% | Divide The Whole By 4 And Multiply The Result By 7 | 175% Of 400 = 100 X 7 = 700 |
| 200% | Multiply The Whole By 2 | 200% Of 400 = 800 |
| 300% | Multiply The Whole By 3 | 300% Of 400 = 1200 |
| 400% | Multiply The Whole By 4 | 400% Of 400 = 1600 |
Direct Multiplication Trick
Since percentage means ‘by the hundred’, a percentage when converted to fractions [link] will have 100 as the denominator and multiply this fraction by a number, makes for easy cancellations of zeros sometimes. View the example below to better understand this
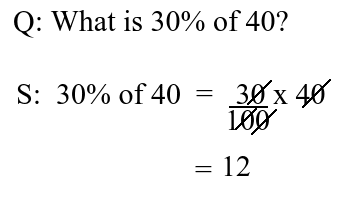
Part of whole
Part of whole percentage problems are ones where the ‘whole’ value and a ‘part’ of it are given to you and you have to find out what percentage the ‘part’ is of the ‘whole’. The problem statement can be presented multiple ways but will always have the part and the whole given away in the problem statement and will require you to find the percentage the part is of the whole.
Example problem statements:
a) 500 is what percent of 7,000?
b) What percent of 250 is 90?
The formula to calculate percentage of part of whole is given by:
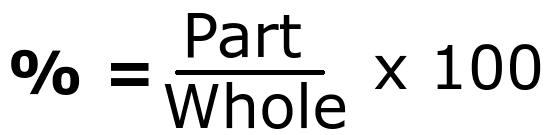
So basically all you have to do is divide the ‘part’ by the ‘whole’ and multiply the result by 100.
Let us solve a few example problems to understand how this formula is applied and to solve step-by-step for better understanding.
Example a) 500 is what percent of 7000?
Solution: Here 500 is the ‘part’ and ‘7000’ is the whole.
Substituting the same in the above formula, we get
Percentage = (Part⁄Whole) x 100
= 555⁄7000 x 100
= 0.07928571428 x 100
= 7.92 %
Example b) What percent of 556 is 77?
Solution: This problem is similar to the above one, just worded differently. Think active and passive voice in English. Instead of directly asking 90 is what percent of 556, the question asks what percent of 556 is 77, essentially asking what percent of ‘whole’ is this ‘part’. Hence, the ‘whole’ is 556 and the ‘part’ is 77
Substituting the same in the formula to calculate percentage of part of whole, we get
Percentage = Part⁄Whole x 100
= 77⁄556 x 100
= 0.1384 x 100
= 13.84%
Let us now try tackling a few more complex word problems of similar kind to better understand and usage of this formula
Example c) The month of January this year saw moderate amount of precipitation. It rained on 11 of the days in the month of January this year. Calculate what percentage of days it rained in the month of January this year?
Solution: January has 31 days, hence the ‘whole’ is equal to 31 and the days it rained is 11, hence the ‘part’ is equal to 11.
Substituting the same in the formula to calculate percentage of part of whole, we get
Percentage = (Part/Whole) x 100
= 11⁄31 x 100
= 0.3225 x 100
= 35.48%
Answer: It rained 35.48% of days in the month of January this year.
Example d) A batch of 1150 students appeared for an examination. Out of which, only 177 students were not able to clear the examination. What percentage of students failed the examination?
Solution: ‘Part’ = 177 students, ‘Whole’ = 1150
Substituting the same in the formula to calculate percentage of part of whole, we get
Percentage = (Part/Whole) x 100
= 177⁄1150
= 0.1017 x 100
= 10.17%
Anwer: 10.17% of students failed the examination
How to Calculate Part Percentage of Whole using a Calculator
Part as a percentage
The next type of percentage problem is one where a part is given as well as expressed as a percentage of the whole and based on that information, we have to calculate the whole. This is essentially a reverse of the previous type of problems. Where previously you were given a percentage and the whole, here you are given the part and the percentage and have to calculate the whole.
Example problem statements:
a) 45 is 10% of what?
b) 60% of X is 200. What is X?
The formula to calculate the whole when a part is given as well as expressed as a percentage:
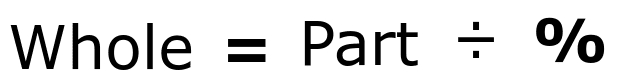
Simply put, this is a reverse of the previous formula. Instead of multiplying the percentage by the whole, here you divide the part by the percentage to get the whole. Keep in mind that like always, percentage is ‘by hundred’. So for instance, if you are dividing a part by 30%, you will divide by 0.3 and not by 30 because 30% = 30 ⁄100 = 0.3
Let us understand the above formula by solving a few examples step-by-step
Example a) 45 is 15% of what?
Solution: ‘Part’ = 45 and Percentage = 15%
Substituting the same in the above formula, we get:
Whole = Part ÷ Percentage
= 45 ÷ 15%
= 45 ÷ 15⁄100
= 45 ÷ 0.15
= 300
Answer: 45 is 10% of 300
Example b) 60% of X is 200. What is X?
Solution: ‘Part’ = 200 and ‘Percentage’ = 60%
Substituting the same in the above formula, we get:
Whole = Part ÷ Percentage
= 200 ÷ 60%
= 200 ÷ 60⁄100
= 200 ÷ 0.6
= 333.33
Answer: X is equal to 333.33
Example c) In a shipment of computer peripherals, 4% of the peripherals were found to be damaged or not in a working condition. If 22 computer peripherals were found to be damaged/not working, what was the total size of the shipment?
Solution: ‘Part’ = 22 and Percentage = 4
Substituting the same in the above formula, we get:
Whole = Part ÷ Percentage
= 22 ÷ 4%
= 22 ÷ 4⁄100
= 22 ÷ 0.04
= 550
Answer: The total size of the shipment was 550 units of computer peripherals
How to Solve Part as a Percentage Problems Using a Calculator
Percentage Change
‘Change’ in mathematics means either an increase or decrease in a new value compared to the original value. To calculate change, the new/final value is subtracted from the old/initial value. If the difference is a positive number, the change is said to be positive or an ‘increase’. If the difference is a negative value, the change is said to be negative or a ‘decrease’. And if the difference is equal to 0, there is said to be no change whatsoever.
Change = Final value – Initial Value
Hence, to calculate percentage change we have to calculate Change ÷ Initial Value and multiply the result by 100
The same can be expressed in an expanded form as:

Some example problems for Percentage Change will look like:
- If the minimum wage is raised from $12 to $15, what is the percentage change?
- The total student count in a class dropped from 300 to 265 over time. What is the percentage change?
The percentage change formula can be used to calculate both percentage increase as well as percentage decrease. As can be seen above if the result -> positive, then it is a percentage increase and if the result -> negative, then it is a percentage decrease.
However, separate formulas for both do exist. The formula for percentage change and percentage increase are the same. Whereas for percentage decrease, the change is calculated by subtracting the Final Value from the Initial Value because for ‘Decrease’, the Final Value is smaller compared to the Initial Value. We will have a look at both the Percentage Increase and Percentage Decrease Formulas separately later.
Let us tackle some example questions for percentage change.
Example a) If the minimum wage is raised from $12 to $15, what is the percentage change?
Solution: As stated in the problem statement, the ‘initial value’ = 12 and the ‘final value’ = 15
Substituting the same in the formula for percentage change, we get
Percentage change = (Final Value – Initial Value)⁄Initial Value x 100
= (15 -12)⁄12 x 100
= 3⁄12 x 100
= 0.25 x 100
= 25
Answer: There was a 25% percentage change/increase in the minimum wage.
Example b) The total student count in a class dropped from 300 to 265 over time. What is the percentage change?
Solution: ‘Initial Value’ = 300, ‘Final Value’ = 265
Substituting the same in the formula for percentage change, we get
Percentage change = (Final Value – Initial Value)⁄Initial Value x 100
=(265 – 300)⁄ 300 x 100
= -35⁄ 300 x 100
= -0.1167 x 100
= -11.67
Answer: There was a percentage decrease of 11.67% in the student count over time.
Example c) The salary of an employee was incremented from $50,000 a year to $55,000 a year. Calculate the percentage of the increment.
Solution: Here the ‘percentage of increment’ means nothing but Percentage Change
The Initial Value = 50,000 and the Final Value = 55,000
Substituting the same in the formula for percentage change, we get
Percentage change = (Final Value – Initial Value)⁄Initial Value x 100
=(55000 – 50000)⁄50000 x 100
=5000 ⁄50000 x 100
=0.10 x 100
= 10
Answer: The salary of the employee was incremented by 10%
How To Calculate Percentage Change in A Calculator
Percentage Increase
In mathematical terms, Increase is the positive difference between the Final Value and the Initial Value. For increase, the Final Value will always be greater than the Initial Value.
Increase = Final Value – Initial Value = New Value – Old Value
Hence, Percentage Increase is nothing but Increase⁄Initial Value x 100
The same can be given in an expanded formula as:

The formula for percentage increase and percentage change is the same as long as Final Value>Initial Value
Let us use the above formula in some example problems and solve them step by step to better understand the Percentage Increase formula
Example a) The floor-to-ceiling height was increased from 10 feet to 12 feet. What is the percentage increase in height?
Solution: ‘Initial Value’ = 10, ‘Final Value’ = 12
Substituting the same in the formula for Percentage Increase, we get:
Percentage Increase = (Final Value – Initial Value)⁄Initial Value x 100
=(12-10)⁄10 x 100
=2⁄10 x 100
=0.2 x 100
= 20
Answer: There is a 20% increase in the floor-to-ceiling height.
Example b) The price of a product was raised from $1,000 to $1,400. Calculate the percentage increase in the price of the product?
Solution: ‘Initial Value’ = 1000, ‘Final Value’ = 1400
Substituting the same in the formula for Percentage Increase, we get:
Percentage Increase = (Final Value – Initial Value)⁄Initial Value x 100
= (1400-1000)⁄1000 x 100
=400 ⁄1000 x 100
=0.40 x 100
=40
Answer: There is a 40% increase in the price of the product.
How to Calculate Percentage Increase in a Calculator
Percentage Decrease
If you are certain that the Final Value is smaller than the Initial Value, you can directly use the Percentage Decrease formula to calculate the percentage change. Since Final Value < Initial Value, Difference = Initial Value – Final Value
And, Percentage Difference = Difference⁄Initial Value x 100
Hence the formula for Percentage Decrease can be given in an expanded form as

Since the value of ‘Initial Value – Final Value’ is positive, we will directly get the percentage difference as the answer as a positive number and not a negative number.
Let us solve a few examples to better understand Percentage Decrease Formula
Example a) In a forest of roughly 9000 trees, only 7000 trees survived the forest fire. What is the percentage decrease in the total number of trees?
Solution: ‘Initial Value’ = 9000, ‘Final Value’=7000
Substituting the same in the formula for Percentage Decrease, we get:
Percentage Decrease =(Initial Value – Final Value)⁄Initial Value x 100
= (9000 – 7000)⁄9000 x 100
= 2000 ⁄9000 x 100
= 0.2222 x 100
= 22.22
Answer: There is a 22.22% decrease in the total number of trees in the forest
Example b) Eric currently weighs 180lbs. He used to weigh 210lbs before joining the gym. Calculate the percentage increase or decrease in Eric’s weight.
Solution: Since Eric’s current weight < Eric’s previous weight, we can say Eric has lost weight/there is a decrease in Eric’s weight. Hence we will calculate the Percentage Decrease here.
‘Initial Value’ = 210, ‘Final Value’ = 180
Substituting the same in the formula for Percentage Decrease, we get:
Percentage Decrease = Initial Value – Final Value⁄Initial Value x 100
=(210 – 180) ⁄210 x 100
=30 ⁄210 x 100
=0.1428 x 100
=14.28
Answer: Eric has lost 14.28% of his original starting weight/Eric has seen a decrease of 14.28% in his weight since starting the gym
How to Calculate Percentage Decrease in A Calculator
How to Add Percentages
When adding or subtracting a percentage to the whole, one crucial point to be kept in mind is that you are adding or subtracting a percentage of the whole to the whole and not just the percentage itself.
Understand the difference in the image below
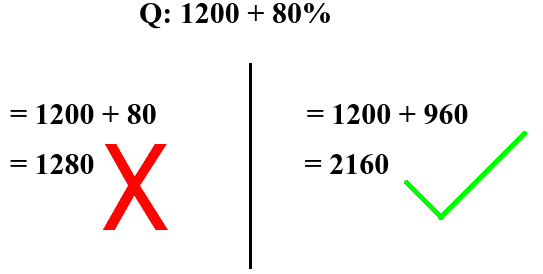
The formula for Percentage Addition is given as:
New Value = Whole + %Whole
Let us better understand how to add a percentage by taking up a few examples
Example a) There were 60 T-Shirts of different sizes and color on display at a boutique department store. The store owner felt this was too little a variety presented to the customers and added 30% more T-Shirts more. What is the total amount of T-Shirts displayed at the store now?
Solution: ‘Whole’ = 60, Percentage = 30%
Substituting in the formula for Percentage Addition, we get:
New Value = Whole + (%Whole)
New Value = 60 + (60 x 30 ⁄100)
= 60 + (60 x 0.3)
= 60 + (20)
= 80
Answer: The total number of T-Shirts on display at the store is 80 now
Example b) A gift shop increased the price of it’s greeting cards by 10% of it’s original price. Earlier it was selling each greeting card for $5. What is the new price of the greeting cards?
Solution: ‘Whole’ = 5, Percentage = 10%
Substituting in the formula for Percentage Addition, we get:
New Value = Whole + (%Whole)
New Value = 5 + (5 x 10 ⁄100)
= 5 + (5 x 0.1)
= 5 + 0.5
= 5.50
Answer: The new price of the greeting cards is $5.50
How to Subtract Percentages
The formula for subtracting a percentage from a whole is the same as above with the only difference between the addition sign being replaced by the subtraction sign
The Formula for Percentage Subtraction is given as:
New Value = Whole – %Whole
Let us understand how to subtract a percentage using few examples
Example a) The stock of a company lost 2.5% of it’s value this past week. It was trading for $340 per stock before the price started falling. What is the current value of the stock?
Solution: ‘Whole’ = 340, Percentage = 2.5%
Substituting in the formula for Percentage Subtraction, we get:
New Value = Whole – (%Whole)
New Value = 340 – (340 x 2.5 ⁄100)
= 340 – (340 x 0.025)
= 340 – 8.5
= 331.5
Answer: The current value of the stock is $331.5
Example b) The value of a car depreciated by 30% a year after it’s purchase. The car cost $45,000 when it was purchased brand new. What is the current cost of the car after the depriciation?
Solution: ‘Whole’ = 45000, Percentage = 30%
Substituting in the formula for Percentage Subtraction, we get:
New Value = Whole – (%Whole)
New Value = 45000 – (45000 x 30 ⁄100)
= 45000 – (45000 x 0.3)
= 45000 – 13500
= 31500
Answer: The current cost of the car after the depriciation is $31,500
How to Add and Subtract Percentages on Calculator
Percent error
Percentage error is an expression of the difference between the approximate value and the exact value in the form of a percentage and is commonly used in different types of research and statistics studies.
Error = | Approximate Value – Exact Value |
The ‘ | ‘ symbol means we take the absolute value of the difference, meaning in simple words that even if the difference is negative, we will drop the negation and take only the value,
For example |5 – 6| = |-1| = 1
We do this because ‘Error’ basically is an calculation of how far away our approximate value is from the Exact Value and irrespective of whether it is positive or negative, we are that many units off from the Exact Value.
For example let’s say you invited all your classmates to your house party and expect 50 people to show up in total.
- Scenario one: Let’s say only 40 people show up to the party. In this case, 10 people less than expected showed up. Hence, your approximation was off by 10 people.
- Scenario two: Let’s say 60 people show up to the party. In this case, 10 people more than expected showed up. Hence here as well, your approximation was off by 10 people
Hence, when calculating Error Percentage we use the following formula
The same can be expressed in an expanded formula as:
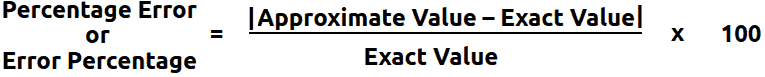
Percentage Error formula without absolutes
The percentage error formula can also be used without absolutes to know if our estimations are low or high.
For example, using absolute values in the house part example given above, we get the percentage error as 20% in both the scenarios. However, if we use the formula without the absolute values, in scenario one we would get the percentage error as 20% and can infer that our estimation was 20% more than the number of people who actually showed up. And similarly in scenario two, we would get the percentage error as -20%, meaning our estimated value was 20% less than the number of people that actually did show up.
Let us solve a few example statements to understand the Percentage Error formula and it’s usage better
Example a) A couple expects 60 people to show up as guests to their wedding and book a hall for the ceremony accordingly. However 75 people show up to their wedding putting a strain on their arrangements. What was the percentage of error in the number of guests who showed up at their wedding?
Solution: Approximate Value = 60, Exact Value = 75
Substituting the above value in the formula for Percentage Error, we get:
Percentage Error = |Approximate Value – Exact Value|⁄Exact Value x 100
=|60 – 75|⁄75 x 100
=|-15|⁄75 x 100
=15⁄75 x 100
=0.2 x 100
=20%
Answer: There was a 20% error in approximation by the couple
Example b) A company declares that the top speed of it’s new vehicle is 140 miles an hour but when tested strictly, it was reported that the top speed achieved was only 128 miles an hour. What is the percentage of error?
Solution: Approximate value = 140, Exact Value = 128
Substituting the above value in the formula for Percentage Error, we get:
Percentage Error = |Approximate Value – Exact Value|⁄Exact Value x 100
=\|140 – 128|⁄ 128 x 100
=\|12|⁄ 128 x 100
=\12⁄ 128 x 100
=0.09375 x 100
=9.375
Answer: The percentage of error is 9.375%
How to Calculate Percentage Error on A Calculator
Percentage Difference
Percentage difference is used when we want to calculate the percentage of the difference between two values divided by the average of those very two values. In percentage difference problem statements, there usually is no way to choose a reference value like in percentage change or percentage error. Hence instead, the average of the two values is taken as the denominator.
The example problem statements for percentage difference look like:
- Find the percentage difference between 400 and 600.
- There were 24 crayons in the first box and 34 crayons in the second box. What is the percentage difference between the two boxes?
The formula for Percentage Difference is given as:
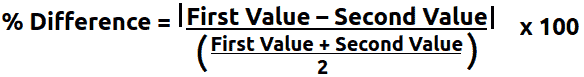
For percentage difference as well, we take the absolute values because unlike percentage change, there is no old or new value as a reference point and hence we can’t say if the difference is up or down, Meaning, if the order or the values were reversed, we would get a positive result for the same subtraction of the two values. Hence, we use absolute values for Percentage difference.
Let us solve the previous example problem statements to better understand how the Percentage Difference formula is calculated.
Example a) Find the percentage difference between 400 and 600
Solution: First value = 400, Second Value = 600
Substituting the values in the formula for percentage difference, we get:
Percentage difference = |First Value – Second Value⁄First Value + Second Value⁄2| x 100
= |(400 – 600)⁄ (400 + 600)⁄2| x 100
=|-200 ⁄ 1000 ⁄2| x 100
=|-200 ⁄500| x 100
=|-0.40| x 100
= 0.40 x 100
= 40%
Answer: The percentage difference between 400 and 600 is 40%
Example b) There were 24 crayons in the first box and 34 crayons in the second box. What is the percentage difference between the two boxes?
Solution: First Value = 24, Second Value = 34
Substituting the values in the formula for percentage difference, we get:
Percentage difference = |First Value – Second Value⁄First Value + Second Value⁄2| x 100
= |(24 – 34) ⁄ (24 + 34)⁄2| x 100
=|-10 ⁄ 58 ⁄2| x 100
=|-10 ⁄29| x 100
=|-0.3448| x 100
=0.3448 x 100
=34.48
Answer: The percentage difference between the two boxes of crayons is 34.48%
Percentage change vs Percentage Error Vs Percentage Difference
Usually, it is mentioned in the problem statement if you would need to be calculating the percentage change, the percentage error or the percentage difference. But sometimes the same might not be mentioned or you might have to apply these formulas in real life usages where it can get quite confusing as to which category your problem falls under.
In such cases remember that:
- Percentage Change is applied when you have an old value and a new value or an initial value and a final value.
- Percentage Error is applicable when you have an approximate value and an exact value.
- Percentage Difference is applicable when you have two values of the same kind with no reference value and hence calculate an average of the two values involved.
Percentage yield
Another commonly used percentage formula is the percentage yield formula used in the fields of chemistry where an element is produced or ‘yielded’ as the direct or byproduct of a chemical reaction. Percentage yield is defined as the percentage of the experimental yield divided by the theoretical yield.
The formula to calculate Percentage Yield is given as:
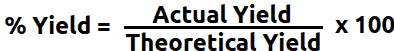
Let us consider a couple of examples to better understand the application and usage of Percentage Yield
Example a) In a chemical reaction of Iron and dilute sulphuric acid, we are expected to get 12 grams of ferrous sulphate as one of the byproducts of the reaction. However when the reaction is actually carried out in a laboratory, it is noted that only 10 grams of ferrous sulphate is produced as the byprodcut. Calculate the percentage yield.
Fe + H2SO4 → FeSO4 + H2
Solution: Theoretical yield = 12, Actual yield = 10
Substituting the two values in the formula for Percentage Yield, we get:
Percentage Yield = Actual Yield⁄Theoretical Yield x 100
=10 ⁄ 12 x 100
=0.8333 x 100
=83.33%
Answer: The percentage yield is 83.33%
Example b) A chemical reaction of Magnesium with dilute nitric acid is expected to produce 1,200mg of magnesium nitrate as the byproduct but when the reaction is carried out in reality, the magnesium nitrate amounts to 1,400mg. What is the percentage yield of this reaction?
Mg + 2HNO3 → Mg(NO3)2 + H2
Solution: Theoretical Yield = 1200, Actual Yield = 1400
Substituting the two values in the formula for Percentage Yield, we get:
Percentage Yield = Actual Yield⁄Theoretical Yield x 100
=1400 ⁄1200 x 100
=1.1666 x 100
=116.66%
Answer: The percentage yield of this chemical reaction is 116.66%
[If the percentage yield > 100%, it means the actual yield was more than the theoretical yield expected]
Percent Off Calculator/Discount calculator
Another very common use of percentages is the calculation of discount and discount percentages. On a near daily basis we see products marketed with different discount percentages or discount amounts. A good understand of the discount formula helps us understand discounts better and make our decisions accordingly.
A ‘discount’ occurs whenever the selling price is lower than the original price.
Hence, Discount Amount = Original Price – Selling Price
Percentage Off is the same as the Discount Percentage on a product and are often used interchangeably.
Percent Off = Discount Percentage
Finding Discount Percentage using Discount Amount & Original Price
There are two types of instances where the discount percentage is applicable in real life. The first is where the discount amount and the original price are known and using the two we have to calculate the discount percentage.
The Percent Off formula or the Discount Percentage is given as:

Let us better understand both the types of problems of Percent Off formula using a couple of example problems
Example a) A soft-toy for kids which sells at $30 was being sold for $22 for Christmas. Calculate the discount percentage on the soft-toy
Solution: Original Price = 30, Selling Price = 22
Discount Amount = Original Price – Selling Price = 30 – 22 = 8
Substituting the above values in the formula for Percentage Discount, we get:
Percentage Discount= Discount Amount⁄Original Amount x 100
= 8⁄ 30 x 100
= 0.2666 x 100
= 26.66%
Answer: There was a discount of 26.66% given on the soft-toy
Example b) A sport equipment that sells for $79 usually had a $13 off on it. Calculate the discount percentage
Solution: Original Price = 79, Discount = 13
Substituting the above values in the formula for Percentage Discount, we get:
Percentage Discount= Discount Amount⁄Original Amount x 100
= 13⁄79 x 100
= 0.1645 x 100
= 16.45%
Answer: There was a 16.45% discount on the sport equipment
How to Calculate Percent Off/Discount Percentage on a Calculator
Finding Discount Amount using Discount Percentage & Original Price
The second is where the discount percent and the original price is supplied and we have to calculate the discount amount using the two
The formula for calculating discount is given as
Discount = Discount% x Original Price
Let us understand the application of the formula using a few examples
Example a) There was a 20% in the price of a product which sells for $800. What is the discount amount?
Solution: Original Price = 800, Discount Percentage = 20
Substituting the values in the discount formula, we get:
Discount = Discount% x Original Price
=20⁄100 x 800
=160
Answer: The discount given was $160
Example b) A book that sells for $15 had a special offer of 40% discount on it. What was the discount offered on the book and what is the new price of the book?
Solution: Original Price = 15, Discount Percentage = 40%
Substituting the values in the discount formula, we get:
Discount = Discount% x Original Price
= 40⁄100 x 15
= 6
Selling Price = Original Price – Discount
=15 – 6
= 9
Answer: The discount given on the book was $6 and the new price of the book after the discount is $9
How to Calculate Discount on a Calculator
Profit Percentage
Another common usage of percentages is in calculation of profit percentages which has wide application in the fields of business and finance. There are two types of problems involved with profit percentages.
The first type is where the profit and cost price are provided and are used to calculate the exact percentage of profit generated from the sale of an item. The second type is where the profit percentage and cost price is provided and we have find the profit using the two.
Finding Profit Percentage
The profit percentage is given by finding the percentage of the profit divided the cost price where
Profit = Selling price – Cost price = Revenue – Total Costs
Hence the profit percentage formula is given as:
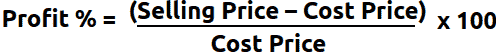
Let us take a couple of examples to better understand profit percentage formula
Example a) The cost of making a pair of shoe is $74 which is then being sold for $125 at the retail store. Calculate the profit percentage on sale of each shoe.
Solution: Cost price = 74, Selling Price = 125
Substituting the above values in the profit percentage formula, we get:
Profit Percentage = (Selling Price – Cost Price)⁄Cost Price x 100
=(125 – 74)⁄ 125 x 100
=51⁄74 x 100
=0.6891 x 100
= 68.91%
Answer: There is a profit percentage of 68.91% on sale of each pair of shoes
Example b) A company generated a total of $1,120,000 in sales the last year. Their total costs for the entire inventory was $950,000. What was their profit percentage?
Solution: Total Cost = 950000, Revenue = 1120000
Substituting the above values in the profit percentage formula, we get:
Profit Percentage = (Revenue – Total Cost)/Total Cost x 100
=(1120000 – 950000) ⁄ 1120000 x 100
=170000⁄1120000 x 100
=0.1789 x 100
=17.89%
Answer: The profit percentage is 17.89%
How to Calculate Profit Percentage on a Calculator
How to find Profit using Profit Percentage and Cost Price
These are the second type of problems where the profit percentage is directly provided and we have to find the amount of profit generated
The formula to calculate profit is given as
Profit = S.P. – C.P. = Profit% x C.P.
Example a) A company generated a profit of 15% on a sale of an item which originally cost $1250 for them to make it. What is the profit generated on this item?
Solution: Cost Price = 1250, Profit Percentage = 15
Substituting the two in the formula for Profit, we get:
Profit = Profit% x Cost Price
= 15⁄100 x 1250
= 0.15 x 1250
= 187.50
Answer: The profit generated on the sale of this item is $187.5
Example b) The cost price of a golf club is $59 which is then sold in retail for a price of $79. Calculate the profit generated on this item.
Solution: Cost Price = 59, Selling Price = $79
Since both the Cost Price and the Selling Price are given, we will directly calculate the Profit as:
Profit = Selling Price – Cost Price
= 79 – 59
= 20
Answer: The profit generated on this item is $20
Loss percentage
Similarly, the loss percentage too is widely used in the field of finance and business. And just like above, there are two types of loss percentage problems. The first type is where the amount of loss and the cost price is provided and we have to calculate the loss percentage and the second type is where the loss percentage and cost price is provided and we have to find the loss amount.
Finding Loss Percentage using Loss and Cost Price
For a loss to occur, the selling price will be less than the cost price.
Loss = Cost Price – Selling Price = Total Cost – Revenue
Hence the Loss Percentage is given as:
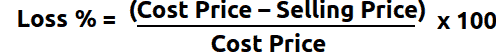
Let us better understand the application of loss percentage by solving a few examples
Example a) A seller produced a shipment of fruits for $25 a box but due to lack of sales and to avoid over-ripening, he had to sell each box of fruits at $18 to clear the stock. What was the loss percentage?
Solution: Cost price = 25, Selling Price = 18
Substituting the above values in the formula for loss percentage, we get:
Loss Percentage = (Cost Price – Selling Price)/Cost Price x 100
=(25 – 18)⁄ 25 x 100
=7⁄ 25 x 100
=0.28 x 100
=28%
Answer: The seller incurred a loss of 28% on each sale
Example b) A small firm invested $40,000 in marketing & advertising, $20,000 in R&D, $50,000 in raw materials and product development and $650,000 as employee salary. The total revenue earned from the sale of this product was $720,000. What was the profit or loss percentage incurred by the firm on this product?
Solution: Total Cost = 40000+20000+50000+650000 = 760000, Revenue = 720000
Revenue < Total Cost, hence the firm incurred a loss
Substituting the values in the formula for loss percentage, we get:
Loss Percentage = (Total Costs – Revenue)⁄Total Costs x 100
=(760000 – 720000) ⁄760000 x 100
=40000 ⁄760000 x 100
=0.052 x 100
=5.2%
Answer: The loss percentage incurred by the company was 5.2%
How to Calculate Loss Percentage on a Calculator
How to Calculate Loss using Loss Percentage
These are the second type of problems where the loss percentage is directly provided in the problem statement along with the cost price and we have to calculate the loss using the two
The formula to calculate loss is given as
Loss = C.P – S.P = Loss% x C.P
Example a) A seller incurred a loss of 6% while selling his product. The cost price of the product was $55. What was the loss incurred on sale of each unit?
Solution: Cost Price = 55, Loss Percentage = 6
Substituting the two in the formula for Loss, we get:
Loss = Loss% x Cost Price
= 6⁄100 x 55
= 0.06 x 55
= 3.3
Answer: The loss incurred on sale of each unit was $3.3
Example b) A bank sold majority of it’s shares at $22 when on the brink of bankruptcy. The shares were trading at $113 a pop before the financial collapse. What was the loss on the value of each share?
Solution: Cost Price = 113, Selling Price = 22
Here, the cost price and the selling price are directly provided in the problem statement itself
Hence, Loss = Cost Price – Selling Price
= 113 – 22
= 91
Answer: There was a loss of $91 on the value of each share
How to Calculate Percentage of Marks
Throughout the world up until high school, the marks scored in an examination are expressed are either expressed as a percentage, percentile or a grade. Very seldom will you hear performance being measured as the raw scores obtained by the student
To calculate the percentage of marks obtained by a student, simply divide the marks scored by the total marks and multiply the result by 100
The formula to calculate percentage of marks is given as:
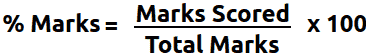
Let us learn how to calculate percentage of marks and the use of the above formula using a few examples
Example a) Jamie scored 543 marks in an examination out of 600. Calculate the percentage of marks scored.
Solution: Marks scored = 543, Total Marks = 600
Substituting the two in the formula to calculate percentage of marks, we get:
Percentage of Marks = Marks Scored⁄Total Marks x 100
= 543⁄600 x 100
= 0.905 x 100
= 90.50
Answer: Jamie scored 90.5% of marks
Example b) Emily scored 1675 marks in an examination out of 2000. Calculate the percentage of marks scored.
Solution: Marks scored = 1675, Total Marks = 2000
Substituting the two in the formula to calculate percentage of marks, we get:
Percentage of Marks = Marks Scored⁄Total Marks x 100
= 1675 ⁄ 2000 x 100
= 0.8375 x 100
= 83.75
Answer: Emily scored 83.75% of marks
How to Calculate Percentage of Marks On Calculator
Percentages, Decimals, Fractions & Ratios Conversion
Percentages can easily be expressed in the forms of decimals, fractions and ratios and vice versa, decimals, fractions and ratios can easily be converted to percentages as well. This interconversion is very helpful in better understanding of percentages. We will learn each type of conversion in below
Decimal to Percentage
To express a decimal as a percentage, all we have to do is multiply the given decimal by 100
For example:
a) 0.22 = 0.22 x 100 = 22%
b) 0.09 = 0.09 x 100 = 9%
The mathematical process behind conversion of decimal to percentage is:
Another simple way to convert a decimal to fraction is to just shift the decimal two places to the the right
Percentage to Decimal
To express a percentage as a decimal, we have to reverse the above process. ‘%’ already means ‘by the hundred’. So the first step to convert a percentage to a decimal is to express the percentage in the fraction form with 100 in the denominator and then carry out the division to complete the conversion
For example:
a) 55% = 0.55
Mathematical process: 55% = 55⁄100 = 0.55
b) 126% = 1.26
Mathematical process: 126% = 126 ⁄100 = 1.26
A simple way to convert a percentage to a decimal is to shift the decimal two places to the left
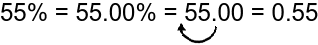
Fractions to Percentage
To convert a fraction to percentage, simply divide the numerator by the denominator and multiply the result by 100
Example a) Convert 12⁄25 to percentage
= 12⁄25 x 100
= 0.48 x 100
= 48%
Example b) Convert 175⁄140 to percentage
= 175⁄140 x 100
= 1.25 x 100
= 125%
Percentage to Fractions
To express a percentage as a fraction, simply express it in it ‘by the hundred’ form and reduce to the lowest terms possible.
Example a) Express 40% as a fraction
40% = 40⁄100 = 2⁄5
Example b) Express 87% as a fraction
87% = 87⁄100
(In the first example, the fraction can be reduced to it’ lowest form. In the second example, the fraction is not reducable. Hence, we leave the second fraction there itself)
Ratio to Percentage
To express a ratio as a percentage, simply express the terms of the ratio as a fraction and multiply it by 100
Example a) Express 1:4 as a percentage
=1⁄4 x 100 = 0.25 x 100 = 25%
Example b) Express 11:10 as a percentage
= 11⁄10 x 100 = 1.1 x 100 = 110%
Percentage to Ratio
To express a percentage as a ratio, express it in the ‘by the hundred’ form and reduce the fraction to the lowest terms possible similar to the Percentage → Fraction conversion explained earlier. Then just one additional step is express the fraction in terms of ratio as N:D
Example a) Express 75% as a ratio
75% = 75⁄100 = 3⁄4 = 3:4
Example b) Express 200% as a ratio
200% = 200⁄100 = 2⁄1 = 2:1
Percentage – Decimal – Fraction – Ratio Conversion Table
| Percentage | Decimal | Fraction | (also commonly worded as) | Ratio |
| 1% | 0.01 | 1⁄100 | 1:100 | |
| 2% | 0.02 | 1⁄50 | 1:50 | |
| 3% | 0.03 | 3⁄100 | 3:100 | |
| 4% | 0.04 | 1⁄25 | 1:25 | |
| 5% | 0.05 | 1⁄20 | 1:20 | |
| 6% | 0.06 | 3⁄50 | 3:50 | |
| 7% | 0.07 | 7⁄100 | 7:100 | |
| 8% | 0.08 | 2⁄25 | 2:25 | |
| 9% | 0.09 | 9⁄100 | 9:10 | |
| 10% | 0.10 or 0.1 | 1⁄10 | One-Tenth | 1:10 |
| 12.5% | 0.125 | 1⁄8 | One-Eight | 1:8 |
| 15% | 0.15 | 3⁄20 | 3:20 | |
| 20% | 0.2 | 1⁄5 | One-Fifth | 1:5 |
| 25% | 0.25 | 1⁄4 | One-forth or a quarter | 1:4 |
| 30% | 0.3 | 3⁄10 | Three-tenth | 3:10 |
| 33.33% | 0.3333 | 1⁄3 | One-third | 1:3 |
| 40% | 0.4 | 2⁄5 | Two-Fifth | 2:5 |
| 50% | 0.5 | 1⁄2 | Half | 1:2 |
| 60% | 0.6 | 3⁄5 | Three-Fifth | 3:5 |
| 66.66% | 0.6666 | 2⁄3 | Two-Third | 2:3 |
| 70% | 0.7 | 7⁄10 | 7:10 | |
| 75% | 0.75 | 3⁄4 | Three Quarters | 3:4 |
| 80% | 0.8 | 4⁄5 | Four-Fifth | 4:5 |
| 90% | 0.9 | 9⁄10 | Nine-tenth | 9:10 |
| 100% | 1 | 1⁄1 | 1:1 | |
| 110% | 1.1 | 11⁄10 | 11:10 | |
| 125% | 1.25 | 5⁄4 | One and a quarter | 5:4 |
| 150% | 1.5 | 3⁄2 | One and a half | 3:2 |
| 175% | 1.75 | 7⁄4 | One and three-quarters | 7:4 |
| 200% | 2 | 2⁄1 | Double | 2:1 |
| 300% | 3 | 3⁄1 | Triple | 3:1 |
Percentages exceeding 100
As we discussed in the very beginning, ‘percentage’ means ‘out of hundred’ or ‘by the hundred’. This confuses a lot of students or beginners when they see values greater than a hundred like 150%, 200% or 1,500% say for example because they assume that 100 is the maximum a percentage of something can go up to. But that is not the case. Percentages can very well go over 100 and they often do in real life.
Percentages going over 100 is a simple concept to grasp and not very different from the basics of percentages we learned earlier.
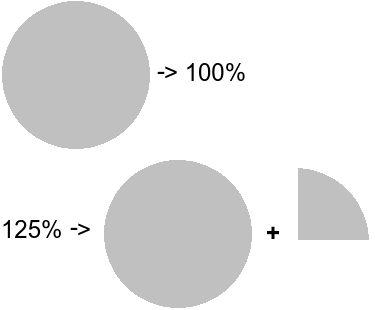
For example, 110% of something would just mean 100% + 10% of that thing. Hence something like 200% would mean double or twice of a value would mean twice or double of that value.
As you can see in the table above, various percentages larger than 100 are presented with their respective decimal and fraction conversions making it easier to grab percentages larger than 100.
Percentages and Pie Charts
Percentages and pie charts are often used alongside each other because pie charts provide excellent visual display of data expressed as percentages. Pie chart is a type of circular graph which makes it very easy to understand data expressed in percentage form. Often time when there are a lot of numbers involved and a variety of different quantites of different percentages, it can get difficult to grasp the percentages as real world quantities. This is where the pie chart is extremely helpful.
Pie chart provides a pictorial representation of the percentages where the ‘pie’ represents the ‘whole’ and the ‘slices’ of the pie represent the ‘parts of the whole’
Formula to convert percentages to a pie chart
A full pie represents 100% of the whole and since the pie is circular in nature (360o), the formula to calculate the slice of the pie chart for part percent is:
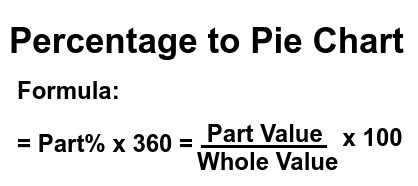
Let us take an example to better understand the formula
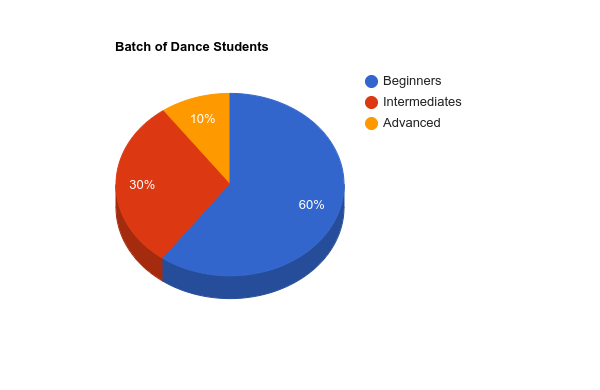
Example: In a group of 200 dance students, 120 students are beginners, 60 students are intermediates and 20 students are advanced dancers. Calculate the percentage of each category and subsequently represent the same as a pie chart
Solution: ‘Whole’ = 200
Beginners = 120 = 120 ⁄ 200 x 100 = 60%
Intermediates = 60 = 60 / 200 x 100 = 30%
Advanced = 20 = 20 ⁄ 200 x 100 = 10%
To get the slice of pie charts:
Beginners = 60% = 60% x 360 = 0.6 x 360 = 216o
Intermediates = 30% = 30% x 360 = 0.3 x 360 = 108o
Advanced = 10% = 10% x 360 = 0.1 x 360 = 36o
Pie chart:
Common Ways To Visualize Percentages
While pie charts might be the most common way to visualize percentages, it is not the one method. There a lot of other graphical representations such as the stacked bar/column, sliding scales, grids, heatmaps etc used to visualize percentages. A chart with the most commonly used types are given below.
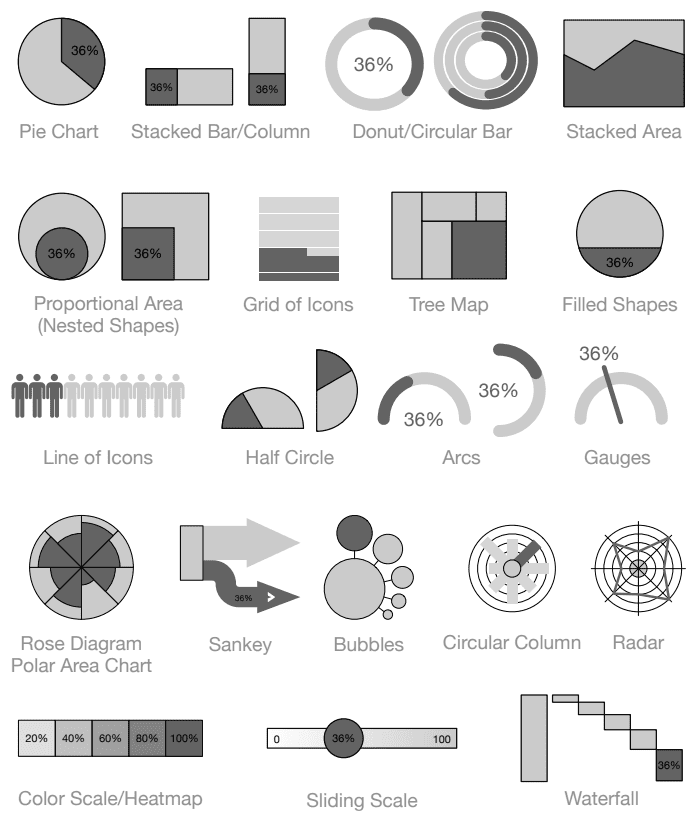
Miscellaneous
Percentile
Percentile is used to express how a score compares to another score in the same set. Percentiles are expressed as a percentage of value that falls under a particular value in a data set.
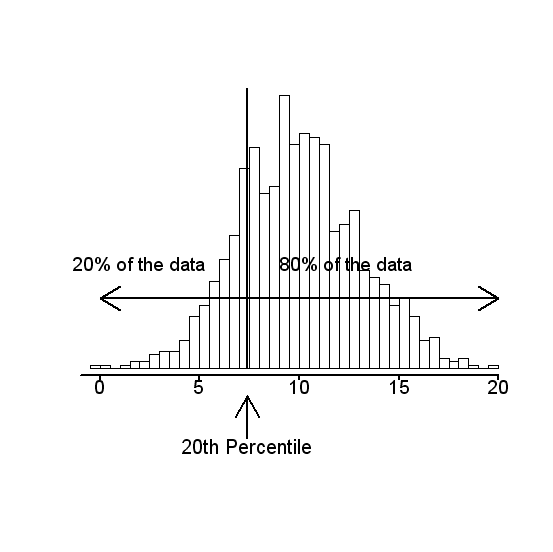
For example, percentiles help us know the percentage of values that fall under a certain value (say all values lesser than 90% of the data set or all values greater than the median of the data set). Percentiles let us know the amount of data set that lie above or below a certain value. Percentiles can also let us know how the average spread of values and how deviated from the normal distribution our scores are.
The formula to calculate Percentile and Percentile Rank is given as
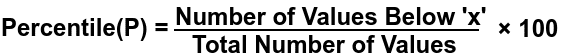
Example a) The age of participants is 22, 33, 17, 43, 28, 41, 57, 32, 77, 30. What is the percentile for the participant aged 43?
Solution: Putting the set in ascending order = 17, 22, 28, 30, 32, 33, 41, 43, 57, 77
Total number of Values = 10, Number of Values below 43 = 7
Substituting the same in the formula for percentile, we get:
Percentile = Number of Values Below “x”⁄Total Number of Values × 100
=7⁄10 x 100
=70%
Answer: The participant aged 43 lies in the 70th percentile
Percentage vs Percentile table
While percentiles make use of percentages, the two are not the same. Following are the differences between percentiles and percentages
| Percentage | Percentile |
| A percentage is a portion of the whole expressed as a fraction of one hundred | Percentile is a comparison of how a certain value stands in comparison to the the other values in the set |
| Percentage does not rank the values involved | Percentile ranks the value in comparison to other values |
| The symbol of percentage is ‘%’ | The symbol of percentile is ‘th’, eg. 70th percentile |
| Percentages can be expressed as decimals as well | Percentiles cannot be expressed as decimals |
| Percentages do not involve normal distribution, quartiles or medians | Percentile is closely related to normal distribution and makes use of quartiles and medians |
| A percentage is an one-to-one comparison of the part to the whole | A percentile is an one-to-many comparison of a value to all the other values in the set |
Per Mille and PPM
‘Per mille’ and PPM(parts per million) are similar to percentages with the difference that ‘per mille’ expresses parts per thousand and PPM as the name implies expresses parts per million. ‘Per mille’ stands for ‘in each thousand’ in Latin.
Per mille is expressed with the symbol ‘‰’
Per mille = 1⁄1000
PPM = 1⁄1000000
Percentage Point
Percentage point is the difference between two percentage. For example, if a percentage increases from 15% to 17.5%, there is said to be a change of 2.5 percentage points. (Not the same as ‘Percentage Difference’ which is percentage of the difference between two values divided by the average of those very two values). Percentage point is a concept widely used in the field of economics but is not restricted to it.
History of percentage
It is difficult to trace back precisely when & where percentages first emerged because decimals and fractions were developed & used by many ancient cultures, independent of each other in most cases, in different timeframes in the past. Given the easy conversion between decimals, fractions and percentages, it is not possible to say when a particular culture started expressing fractions or decimals as percentages.
The Egyptians hieroglyphs used a purely decimal system since around 3000 B but around c. 1000 BC can be seen making use of Egyptian fractions. In the book ‘ One to Zero. A Universal History of Numbers’ Georges Ifrah talks about the decimal system used in Ancient Egypt “From the end of the fourth millennium B.C., the Egyptians used a written numeration that was integrated into hieroglyphic writing and enabled them to note whole numbers up to and even beyond 1,000,000. It had a decimal base and employed the additive principle. There was a special sign for each of the first seven powers of 10: for 1, a vertical line; for 10, a sign with the shape of an upside-down U; for 100, a spiral; for 1000, a lotus blossom; for 10,000, a raised finger, slightly bent at the tip; for 100,000, a tadpole; and for 1,000,000, a kneeling genie with upraised arms…This hieroglyphic numeration was a written version of concrete counting systems using pebbles, sticks, or other material objects. It was based on the additive principle: to represent a number, the sign for each decimal order was repeated as many times as necessary. To make it easier for the reader to count these repeated signs, they were often placed in groups of two, three, or four, arranged vertically, as shown in figure”
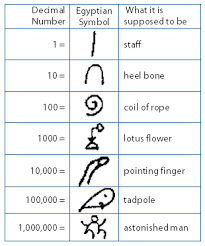
^Georges Ifrah: From One to Zero. A Universal History of Numbers, Penguin Books, 1988, ISBN 0-14-009919-0, pp. 200–13 (Egyptian Numerals)
The Cretan hieroglyphs whose numerals are closely based on the Egyptian model also used a purely decimal system. The Hittite hieroglyphs (1500 BC) were also strictly decimal. George Ifrah continues , “The three Cretan numerations of the second millennium B.C. used exactly the same principle as the Egyptian hieroglyphic notation, and this principle was not changed in any way during their existence. Nor were Cretan writing signs and numerals replaced with a cuneiform system, as occurred in Mesopotamia. Like the Egyptian hieroglyphic notation, these numerations had a decimal base and used the procedure of juxtaposing signs by addition. And the only numbers with special signs were 1 and the powers of 10. The sign for 10,000 in Linear B, formed by placing a horizontal line inside the sign for 1000, obviously represented a use of the multiplicative principle (10,000 = 1000 x 10), since the horizontal line was the sign for 10….Like the Egyptian hieroglyphic system and the three Cretan nu-merations, the Hittite hieroglyphic numeration was strictly decimal and additive, and it had special signs only for powers of 10.”
The Egyptians were not the only ones to use decimals and fractions though, around the same era (c. 3300 – 1300 BCE), the Indus Valley Civilization used standardized weights in the ratios of 1/20, 1/10, 1/5, 1/2, 1, 2, 5, 10, 20, 50, 100, 200, and 500 and their standardized ruler was divided into ten equal parts possibly implying the use of fractions. During the Bronze Age cultures of the Greece, the number system of Greece also used power of ten.
The use of decimals and fractions can also be seen in the Vedas (1700 – 900 BCE) although the origin of them in the Vedas are unknown and around AD 500, modern expression of fractions known as bhinnarasi seems to have originated in India in the work of Aryabhatta (c. AD 500), Brahmagupta (c. 628), and Bhaskara (c. 1150) although they did not use the bar when writing the fractions.
The etymology of the modern word of ‘percent’ and consequently ‘percentages’ stem from Latin term ‘per centum’ meaning ‘by the hundred’. The Romans made use of fractions in the multiples of 1⁄100 before they discovered and used the decimal system. The Romans did not use numerals to indicate fractions, but instead used words to indicate parts of a whole.
As stated on the university of Hawaii’s website, “A unit of weight was the ‘as’ and the ‘uncia’ (from which we have the word “ounce”) was a twelfth part of the as. Multiples of the ‘as’ were indicated using the following scheme, in which a denarius represents 16 asses. Denarii semuncia sicilicus represented 1/24 + 1/48 of a denarius or 1/16 denarius, or 1 as. Denarii uncia semuncia represented 1/12 + 1/24 of a denarius or 1/8 denarius, or 2 asses. Denarii sextans sicilicus represented 1/6 + 1/48 of a denarius, or 3/16 denarius, or 3 asses. Denarii deunx sicilicus represented 11/12 + 1/48 of a denarius, or 15/16 denarius, or 15 asses [Smith vol. 2, pages 208-209].”
This use of fractions can also be seen with Augustus levying the centesima rerum venalium tax on goods. Jane Gardner presents a well-worded description of the same in the book ‘The Augustan Succession’ under the section ‘Liability to Inheritance Tax in the Roman Family’
“In the year 5 CE Augustus instituted a treasury for the payment of military retirement benefits, the aerarium militare, funded by a sales tax or vicesima of 5 per cent and by a tax on inheritances by will. The political purpose of this measure needs no comment here. For the administration of the collection of the inheritance tax there is ample evidence in legal and epigraphic sources and in papyri.”
The oldest existence of a symbol used to express to percentages in writing can be traced back to 1300 – 1400s with the oldest being a symbol ‘p 100’ with the descender of the ‘p’ crossed by a horizontal strike in the 1339 arithmetic text of Rara Arithmetica, page: 437. Such a letter p (with it’s descender crossed horizontally or diagonally was used in the Medieval and Renaissance Paleography to express ‘per’ (or alternatively: par, por, pur)

Later in 1425, in the publication of Rara Arithmetica, we see the expression of percentage in a different symbol (the abbreviation “pc” with a tiny loop or circle)

Around 1600s this abbreviation of a looped ‘pc’ evolved to a horizontal fraction as can be seen in the Rara Arithmetica publication of 1684.
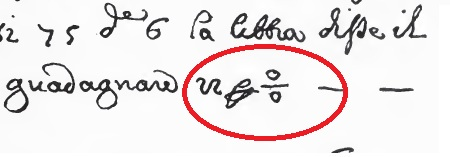
Over time the horizontal percentage symbol transformed into the modern symbol we use today with a slash/solidus